The New International Date Line
This is where the International Date Line is right now:
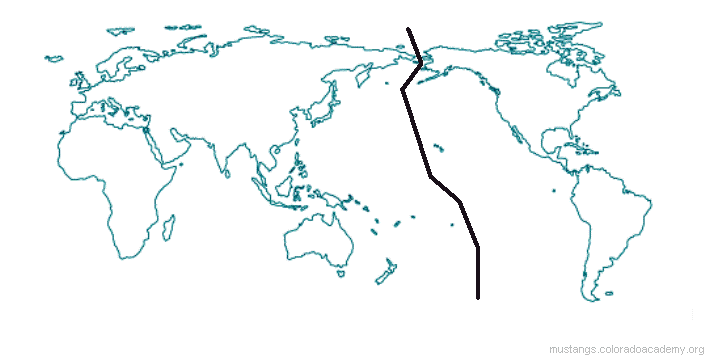This is where the International Date Line should be:
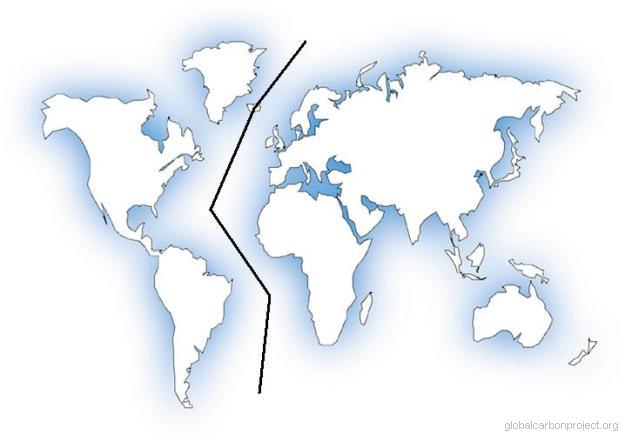
Prime Number Formula For The Planck Constant
Let p be a prime number. Then the prime numbers p1 = 2, p2 = 3, p3 = 5, p4 = 7.... Now let
$$
\begin{array}{lcl}
\displaystyle x
&=&
\sqrt{ \sum_{i=1}^{153} \frac{(p_{i+1}-p_{i})}{(2-(p_{i+1}-p_{i}) \% 2)10^{i-1}} }
\\
\\
&=&
\sqrt{ \frac{(3-2)}{(2-1)10^0} + \frac{(5-3)}{(2-0)10^1}+ \frac{(7-5)}{(2-0)10^2}+ \frac{(11-7)}{(2-0)10^3}+ \frac{(13-11)}{(2-0)10^4}+ \frac{(17-13)}{(2-0)10^5}+\cdots }
\\
\\
&=&
\sqrt{ \frac{1}{10^0} + \frac{1}{10^1}+ \frac{1}{10^2}+ \frac{2}{10^3}+ \frac{1}{10^4}+ \frac{2}{10^5}+ \frac{1}{10^6}+ \frac{2}{10^7}+ \frac{3}{10^8}+ \frac{1}{10^9}+ \frac{3}{10^{10}}+ \frac{2}{10^{11}}+\cdots }
\\
\end{array}
$$
= √ (1.11212123132123313213234212127231513323315121662123153331321572127351234332342451513234212642423619353313533133216512331623454543324324275615121572127212...)
The actual number is infinitely long, but after 153 digits (152 decimal places), base-10 is no longer sufficient.
The results for now, therefore, are:
$$
\begin{array}{lcl}
\displaystyle x
&=&
\displaystyle1.0545715866271161452187407321621 \dots,
\\
\displaystyle 2\pi x
&=&
\displaystyle6.6260686984645606473287437174211 \dots.
\end{array}
$$
The \(1/10^{34}\) and the units aren't accounted for yet. I'm working on it. It's interesting to note how only 9 of the 10 numbers are used though.
I'd like to thank John Walker's Solar System Live page and JPL at NASA.
